International Planning Competition 2018
Probabilistic Tracks
The International Planning Competition is organized in the context of the International Conference on Planning and Scheduling (ICAPS). It empirically evaluates state-of-the-art planning systems on a number of benchmark problems. The goals of the IPC are to promote planning research, highlight challenges in the planning community and provide new and interesting problems as benchmarks for future research.
Since 2004, probabilistic tracks have been part of the IPC under different names (as the International Probabilistic Planning competition or as part of the uncertainty tracks). After 2004, 2006, 2008, 2011 and 2014, the 6th edition of the IPC probabilistic tracks will be held in 2018 and conclude together with ICAPS, in June 2018, in Delft (Netherlands). This time it is organized by Thomas Keller, Scott Sanner and Buser Say.
The deterministic part of IPC is organized by Florian Pommerening and Alvaro Torralba. You can find information about it on ipc2018-classical.bitbucket.io.
The temporal part of IPC is organized by Andrew Coles, Amanda Coles and Moises Martinez. You can find information about it on ipc2018-temporal.bitbucket.io.
To stay up-to-date with the probabilistic tracks, register for the mailing list at https://groups.google.com/forum/#!forum/ipc2018-probabilistic
Preliminary Schedule
| Event | Date |
|---|---|
| Call for domains / expression of interest | July 14, 2017 |
| Domain submission deadline | November 30, 2017 |
| Demo problems provided | January 17, 2018 |
| Expression of interest | February 4, 2018 |
| Initial planner submission | April 5, 2018 |
| Final planner submission | May 3, 2018 |
| Planner abstract submission deadline | May 20, 2018 |
| Contest run | May-June, 2018 |
| Results announced | June, 2018 |
Tracks
The competition is run in the tracks discrete MDP, continuous MDP and discrete SSP. These tracks focus on the maximization of the expected reward in a discrete or continuous environment (discrete and continuous MDP tracks) or on the minimization of the expected cost to reach a goal (discrete SSP track).
Additionally, there are the novel discrete data-based MDP and continuous data-based MDP tracks, which are versions of the discrete and continuous MDP tracks where a set of sample traces is provided as input rather than a declarative model of the MDP.
Updates: The data-based tracks as well as the discrete SSP track have been cancelled due to a lack of participants. The continuous MDP track has been postponed to 2019. Please contact Scott Sanner if you wish to stay up-to-date.
Discrete MDP Track
- Organizer: Thomas Keller (University of Basel)
- Model:
- Markov decision process (MDP)
- fixed initial state
- finite horizon
- no discounting of rewards (the discount factor is 1)
- binary variables (enum-valued variables are optional, a compilation is provided)
- discrete transitions
- conditional (state-dependent) rewards
- action preconditions
- no dead-ends (there is an applicable action in every reachable state)
- Resources:
- memory limit of 4.5Gb
-
time limit depends on the
instance
As a rule of thumb, we provide 75*2.5*H seconds for each instance (exceptions are possible), where H is the finite horizon. As a result of a discussion among the participants and organizers, we decided to increase the average deliberation time significantly (this was 50*H seconds before).
- Evaluation:
- 75 runs per instance have to be completed in time
- We provide a minimal reference policy for each instance. As in IPC 2011 and 2014, we use the better of a random policy and a noop policy (if noop is always legal).
-
The instance score of a planner for
a given instance is 0 if less than 75 runs were
completed in time or if the average
accumulated reward
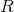 of the 75 runs of
the planner is less than or equal to the average
accumulated reward of the minimal reference policy
of the 75 runs of
the planner is less than or equal to the average
accumulated reward of the minimal reference policy
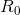 , and
, and
otherwise, where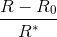
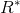 is the highest average accumulate reward
of all participants.
is the highest average accumulate reward
of all participants.
- The total score of a planner is the sum of its instance scores (this is different from IPC 2011 and 2014) and hence ranges between 0 and the number of instances at IPC 2018. To make sure that all domains are equally important, there is an equal number of instances for each domain.
- Minimal input language
requirements:
-
We use the same fragment of RDDL as
in IPC 2011 and 2014 with the changes listed
below.
Please have a look at the demo domains for examples of these changes!-
action-preconditions and
state-invariants sections
The most important addition to the fragment of RDDL that was used in the previous competitions is the action-preconditions section. At IPC 2011 and 2014, there was a state-action-constraints section that could be used to describe invariants, static preconditions and action preconditions, even though the latter was not used in any domain. As it turns out, it is problematic semantically to combine state invariants and action preconditions in one section, since the latter must be checked by the planner at runtime, whereas the former can be assumed to be true (and it is impossible to check all successor states if a state invariant is violated). We therefore decided to remove the state-action-constraints section and replace it with an action-preconditions section and a state-invariants section. The action-preconditions section contains a set of Boolean formulas, each of which must be true for an action to be applicable in some state, and the state-invariants section contains formulas that can be assume to be true in all reachable states. -
no max-nondef-actions entry in
the instance
Related to the former bullet point, the max-nondef-actions entry of the instance block was an additional way of restricting applicable actions. Since this can be done equivalently in the action-preconditions section, the max-nondef-actions entry is omitted. -
type hierarchy
This is not a new concept in RDDL, but it hasn't been used at IPC 2011 and 2014. -
KronDelta is now optional
In an attempt to make modeling domains with RDDL easier, KronDelta is now optional. This means that, whenever a value is used in place of a probability distribution, it is assumed that, in place of the value, there is a KronDelta distribution that places all weight on that value. -
& for logical
conjunctions (instead of
^)
For consistency with the sign for disjunctions (|), we use & rather than ^ for logical conjunctions. -
no equals sign following the
requirements keyword
Again, this is for consistency reasons (all other RDDL keywords that specify a list do not use the equals sign either). -
no non-fluents section
We believe that the separation of a planning task into domain, non-fluents and instance does not have significant advantage over the separation into domain and instance. Since the latter is well-known from all other planning tracks of the IPC, we move the objects and non-fluents block from the non-fluents section to the instance section.
-
action-preconditions and
state-invariants sections
- The PDDL description was removed since no participant decided to use PDDL as input language.
-
Demo domains and instances:
- RDDL
- PDDL domains removed.
-
We use the same fragment of RDDL as
in IPC 2011 and 2014 with the changes listed
below.
Registration
Unlike in IPC 2011 and 2014, competitors do not run their planners themselves. This time, the competitors must submit the source code of their planners, and the organizers will run all planners on the actual competition domains/problems, unknown to the competitors until this time. This way, no fine-tuning of the planners will be possible.
All competitors must submit an abstract (max. 300 words) and a 4-page paper describing their planners. After the competition we encourage the participants to analyze the results of their planner and submit an extended version of their abstract. An important requirement for IPC 2018 competitors is to give the organizers the right to post their paper and the source code of their planners on the official IPC 2018 web site.
Registration Process
There are three important dates for the registration of planners (the deadlines are only important for the discrete tracks; information on deadlines for the continuous MDP track will follow later). This starts with an expression of interest in participation in one or more tracks, which is due February 4, 2018. Please let us know which tracks you are interested in and which input language you are planning to use by sending a mail to ipc2018-probabilistic-organizers@googlegroups.com.
We will use the container technology "Singularity" this year to promote reproducibility and help with compilation issues that have caused problems in the past.
The second step is to register your planner until April 5, 2018. To do so, send an email to ipc2018-probabilistic-organizers@googlegroups.com and let us know if you wish to use a mercurial or a git repository and provide us your bitbucket user names. We will then set up your repository on bitbucket, give you write access and let you know that you can submit your code to the repository. To do so, create one branch per track you want to participate in and name it according to the following list:
- ipc2018-disc-mdp (discrete MDP track)
- ipc2018-disc-ssp (discrete SSP track, canceled)
- ipc2018-cont-mdp (continuous MDP track, postponed to 2019)
We will build all planners once a day and run them on a number of test cases. You can see the results for your planner on the build status page. Test your Singularity file locally (see below) and make sure it passes our automated tests. Please note that the test runs are shorter than the actual competition runs (only 10 iterations instead of 75, and tighter time constraints). The quality of your planner's results is not important at this point, so don't worry if the time limit seems unreasonably small.
A planner is officially registered in a track if it has a green box for that track on the build status page on April 5. You can still make any code changes you want until the final submission deadline on May 3. The build status on the website will update (once a day) when you push new changes the registered branches.
On the final submission deadline on May 3, 2018, we will change your access rights to the repository (or repositories) from write access to read access. If you find any bugs in your code afterwards, you can still fork the repository, fix the bug in the fork and create a pull request for the ipc2018-probabilistic-bot. If we detect any bugs while running your code, we'll let you know and you are also allowed to provide a bug fix. However, only bug fixes will be accepted after the deadline (in particular, we will not accept patches modifying behavior or tuning parameters).
Details on Singularity
In an effort to increase reproducibility and reduce the effort of running future IPCs, we are using software containers that contain the submitted planner and everything required to run it. We are using Singularity which is an alternative to the well-known Docker. Singularity (in contrast to Docker) is specifically designed for scientific experiments on HPC clusters and has low overhead.
Singularity containers can be viewed as light-weight alternatives to virtual machines that carry a program and all parts of the OS that are necessary to run it. They can be based on any docker image. We created an example submission (Singularity file) that uses the latest Ubuntu as a basis and uses apt-get to install required packages for Prost. It then builds the planner from the files that are next to the Singularity file in the repository.
In the following, we collect and answer frequently asked questions about Singularity. We'll update this section as we get more questions. If you run into problems using Singularity and your problem is not answered here, let us know.
You can install Singularity locally with the following commands (See the Singularity quick start guide for more details):
sudo apt install automake libtool
git clone https://github.com/singularityware/singularity.git
cd singularity
git checkout vault/release-2.4
./autogen.sh
./configure --prefix=/usr/local
make
sudo make install
To test your Singularity script, please install Singularity (see above) and rddlsim, start rddlsim on the provided demo instances and run the following commands (replacing our demo submission with your repository):
git clone https://bitbucket.org/ipc2018-probabilistic/demo-submission --branch ipc2018-disc-mdp
sudo singularity build planner.img demo-submission/Singularity
mkdir rundir
RUNDIR="$(pwd)/rundir"
singularity run -C -H $RUNDIR planner.img recon_demo_inst_mdp__1 2323
The last command also shows how we will call the container during the competition: the parameter "-H" mounts the user's home directory. The parameter "-C" then isolates the container from the rest of the system. Only files written to the mounted directory will be stored permanently. Other created files (for example in /tmp) only persist for the current session and are cleaned up afterwards. When running the container on two instances at the same time, their run directories and sessions will be different, so the two runs cannot interact. The container itself is read-only after its creation.
We will also build your code about once per day and show the results for all planners on the build status page
/tmp/tmpPlease contact us if your license does not permit you to package the library into the container.
If we can acquire a license, we will mount the
installation files for the library while building
the container. You can then copy the installation
file into the container in the %setup
step and install it in the %post
step.
%setup section will copy the files
from the correct branch into the container. In the
%post section you can then build your
planner in the directory /planner.
Bootstrap:
docker is then parsed as Bootstrap:
docker\r and not recognized. Using
Linux-style line endings should fix the issue.
Competition Setup
All (discrete & continuous) tracks
To estimate the quality of the computed policies, we execute the policies 75 times and use the average as a metric for the policy's quality. We do so by having your planner interact as a client with the rddlsim server. Detailed information on the protocol that is used to exchange messages between client and server can be found in the file PROTOCOL.txt in the root directory of rddlsim.
Here, we just discuss the changes for IPC 2018:
- In the session-request message that is sent initially from the client to the server, the client has to provide the input language it uses (rddl or ppddl).
- The answer of the server is the session-init message. While domain and instance have been provided as two files in previous competitions, the server provides them for IPC 2018 with the session-init message in the task tag (this allows us to determine exactly when each participant starts to plan).
- As rddlsim communicates with its clients via XML messages, "<" and ">" are replaced by the strings "\<" and "\>", respectively (sending "<" and ">" would invalidate the XML). The domain and instance descriptions are therefore sent in base64 encoding which you have to decode in your planner. You should be able to find code that does this for most programming languages. However, if you encounter problems with this, please let us know and we'll try to find a solution.
- Finally, round-request messages must contain an additional tag execute-policy with content "yes" or "no". If set to "yes", the next round is "executed" and is therefore regarded as one of the 75 runs that are used to compute instance scores. Otherwise, the round is a simulation round that does not count (you can find the reason for this change here).
If you want to test your planner locally, please update to the latest version of rddlsim, recompile and start the server with the command
./run rddl.competition.Server PROBLEM_DIR PORT 75 1 1 1800 ./ 1
where PORT is the port where the client can connect
(by default, this is 2323) and where 1800 is the
allowed time in seconds (this will differ from
instance to instance at IPC 2018).
PROBLEM_DIR is
a directory that contains two subdirectories "client"
and "server". The "client" directory contains the rddl
or pddl files that are sent to your planner as part of
the session-init message, and the "server"
subdirectory contains matching rddl files that are
used by the server. Even though it is still possible
to set PROBLEM_DIR to a directory that contains rddl
files that are shared by client and server, the
tarballs that provide the demo domains and instances
all contain separate client and server files.
Competitors
5 different planners and 7 planner variants
participated in the probabilistic discrete MDP track
of IPC 2018. Planner abstracts for each planner are
available as a planner abstract booklet or as
individual files linked below. The source code of all
entries is publicly available on bitbucket.
To build the planners, follow the instructions
provided in the FAQ on
Singularity. Note that some planners require the
LP solver Gurobi
to compile. To build these planners, acquire a Gurobi
license (a free academic license can be obtained on
request), download the installation files, and move
both to the directory /third-party or
change that path in the Singularity file.
Some planners still had bugs in the final runs of the competition, but we encourage competitors to provide bug free versions in the repositories. The revision at the tip of the track's branch (ipc2018-disc-mdp) includes all fixes. We recommend to use this version in all experiments. To see the changes compared to the competition, compare to the tag ipc2018-disc-mdp-competition. If this tag does not exist, no bug fixes were provided.
-
A2C-Plan (code)
by Anurag Koul, Murugeswari Issakkimuthu, Alan Fern and Prasad Tadepalli
(planner abstract) -
Imitation-Net (code)
by Murugeswari Issakkimuthu, Alan Fern and Prasad Tadepalli
(planner abstract) -
Prost-DD-1 (code) and
Prost-DD-2 (code)
by Florian Geißer and David Speck
(planner abstract) -
Random-Bandit (code)
by Alan Fern, Murugeswari Issakkimuthu and Prasad Tadepalli
(planner abstract) -
Conformant-SOGBOFA-F-IPC18 (code) and
Conformant-SOGBOFA-B-IPC18 (code)
by Hao Cui and Roni Khardon
(planner abstract) -
Baseline: Prost-2011 (code) and
Prost-2014 (code).
The winners of the previous two competitions serve as a baseline. The used versions are based on the state of the Prost planner repository at the time of the competition, so all bug fixes committed in the meantime are included in these planners.
Domains
The eight domains that were used in the competition exist in four different yet equivalent versions:
-
the original RDDL model, potentially including
interm-fluents and enums (files)
(not used by any competitor) -
an equivalent RDDL model without interm-fluents (files)
(used by A2C-Plan, Imitation-Net, both Prost-DD versions and Random-Bandit) -
an equivalent RDDL model without enums (files)
(not used by any competitor) -
an equivalent RDDL model without enums and with
reformulated action preconditions (files)
(used by Conformant-SOGBOFA-F-IPC18 and Conformant-SOGBOFA-B-IPC18)
|
Academic Advising Based on the Academic Advising IPC 2014 domain by Libby Ferland and Scott Sanner. In this domain, a student may take courses at a given cost and passes the course with a probability determined by how many of the prerequisites they have successfully passed. A student also receives a penalty at each time step if they have not yet graduated from their program (i.e., completed all required courses). We allow multiple courses to be taken in a semester in some instances. Furthermore, instances differ in the depth of the course dependency DAG, the number of courses, in the cost of taking or retaking a course, in the number of program requirements and in the horizon. Instances were created such that a policy that ignores all dependencies between courses and takes each course that is a program requirement until it succeeds is better than a policy that does nothing at all. The expected reward of this policy is reported in the instance files. |
|
Chromatic Dice Chromatic Dice is a variant of the popular dice game Yahtzee (also known as Kniffel). The most important difference is that dice show colored values upon rolling, where the color is independent from the value (e.g., the same die can come up with a blue 6 and a red 6 in two consecutive steps). The colors allow for some additional categories in a new middle section (one for each color where the sum of all values with a certain color count) and five new categories in the lower section (color versions of three and four of a kind, full house, flush and rainbow). Like the "upper" section (with categories ones, twos, etc), the new middle section allows for a bonus if the assigned dice meet certain criteria. Since this domain is modelled without integer-valued variables, we cannot encode a condition for the bonus that relies on the sum of all entries in the section (each entry is directly converted into immediate reward which cannot be accessed later). Instead, we take a probabilistic approach, where we keep track of levels that define a probability that the bonus is received. If four or five dice count towards one of the categories, the level increases, and if one or two dice count it is decreased. There is such a level both for the upper and middle section, and both boni are granted (or not) at the end of a run. Even though the optimal policy in the MDP version of Chromatic Dice that is considered here is not optimal in a version of the original problem (i.e., a game with one or more adversaries), it is close enough to make for a challenging player that is non-trivial to defeat. |
|
Cooperative Recon Based on the Recon IPC 2011 domain by Tom Walsh. In the Cooperative Recon domain, the planner controls one or more planetary rovers that examine objects of interest in order to detect life and take a picture of it. As in the Recon domain of IPC 2011, first has to be detected before life is detected, and negative results (one for life, two for water) contaminate the object of interest such that no life can be detected. The main changes compared to the IPC 2011 Recon domain that have been realized are as follows:
|
|
Earth Observation Based on the paper "An Experimental Comparison of Classical, FOND and Probabilistic Planning" by Andreas Hertle, Christian Dornhege, Thomas Keller, Robert Mattmüller, Manuela Ortlieb, and Bernhard Nebel (KI 2014). The Earth Observation domain models a satellite orbiting Earth. It can take pictures of the landscape below with a camera. The landscape is subdivided into square regions of interest forming a grid wrapped around a cylindrical projection of the Earth surface. The camera focuses on one region at a time and can be shifted north or south. It can take a picture of the region currently in focus. The focus may not be shifted while taking a picture. Regardless whether the focus is shifted or a picture is taken, the satellite moves eastward around Earth, shifting the focus one grid cell to the east in addition to the other effects in each step. The objective is to take pictures of certain regions in a limited timeframe with as few shifts and as quick as possible. Taking a picture of a region does not guarantee good image quality: the worse the weather, the lower the chance of success. Over time the visibility in each region can change probabilistically. Changes between similar levels of visibility are more likely than vast changes. |
|
Manufacturer In this domain, the agent manages a manufacturing company that buys goods to use them in the production of other goods. The relationship between the various goods (i.e., which good is required in the production of which other good) takes the form of a directed acyclic graph. Prizes of goods are determined stochastically by being drawn towards a long-term trend price level with higher probability than moving away from it. The accumulated reward encodes the bank account of the company, i.e., all monetary costs in the domain incur a negative reward while selling goods yields a positive reward. This domain is modular in the sense that additional options are available in more challenging instances, all of which have in common that the agent has to take an immediate cost for an increased long-term reward. This is already true for the basic concept of buying goods (cost) to produce another good that can be sold for more than the sum of the costs. The following modules (that can be mixed) are available:
|
|
Push Your Luck As the name suggest, Push Your Luck is an artificial version of a "push your luck" game like, for instance, Can't Stop. The main challenge of push your luck games is to determine the optimal moment to stop a repeated stochastic process. In case of the Push Your Luck domain, the player may roll one or more dice repeatedly. Each rolled face is marked if it hasn't been marked before, and all numbers are unmarked if the player chooses to cash out its reward, if a number is rolled that is already marked or if two rolled dice come up the same face. The reward the player obtaines upon cashing out corresponds to the product over the value of all marked faces, so it grows exponentially in the number of consecutive die rolls (by default, the value of the face of a 6-sided die equals half the number shown on the die, and the default value of a 10- or 20-sided die is 0.25 plus a quarter of the shown die value. On the other hand, the probability to hit a previously rolled number increases with the number of consecutive die rolls. |
|
Red-finned Blue-eye Created in collaboration with Iadine Chades, based on the paper "Finding the best management policy to eradicate invasive species from spatial ecological networks with simultaneous actions" by Sam Nicol, Regis Sabbadin, Nathalie Peyrard and Iadine Chades (Journal of Applied Ecology 2017). Red-finned blue-eye (Scaturiginichthys vermeilipinnis) are a species of fish that are endemic to seven artesian springs in the Edgbaston Reserve in Central Queensland, Australia. The species is critically endangered due to competition by the invasive eastern mosquitofish (Gambusia holbrooki). The Red-finned Blue-eye domain tackles the problem of eradicating the invasive Gambusia from the habitat of the red-finned blue-eye. The springs are disconnected during the dry season, but get connected in the rain season which allows the Gambusia population to spread from spring to spring and replace the red-finned blue-eyes. To prevent the extinction of the red-finned blue-eye species, springs with Gambusia population can be poisened (with a high success probability but a penalty for using poison), the Gambusia population can be removed manually (with a lower probability of success and more required effort, but without incurring a penalty) or red-finned blue-eyes can be translocated to a spring without any fish population (which takes so much effort that it can only be done once every few years). |
|
Wildlife Preserve Created in collaboration with Fei Fang and Thanh Hong Nguyen, based on the papers "When Security Games Go Green: Designing Defender Strategies to Prevent Poaching and Illegal Fishing" by Fei Fang, Peter Stone and Milind Tambe (IJCAI 2015) and "Analyzing the Effectiveness of Adversary Modeling in Security Games" by Thanh H. Nguyen, Rong Yang, Amos Azaria, Sarit Kraus and Milind Tambe (AAAI 2013). The aim of the Wildlife Preserve domain is to protect a wildlife preserve from poachers by sending available ranger to areas. Poachers attack parts of the preserve depending on their preferences and an expectation where rangers will likely show up. This expectation is computed by exploiting the assumption typically taken in Stackelberg Security Games that the defender’s (i.e., rangers) mixed strategy is fully observed by the attacker, and memorized for a predefined number of steps. In each step, the planner obtains a reward for each area that has not been attacked undefended, and a penalty for each area that has. The challenge is to predict where poachers will attack with high probability and to lure the poachers that observe each step of the rangers into attacking an area where they are caught. A poacher that has been caught does not attack in the next step. |
Results
The results were presented at the 28th International Conference on Automated Planning and Scheduling on June 29 in Delft (presentation slides). Per domain scores and the total score of each participating planner in the discrete MDP probabilistic track of IPC 2018 are summarized in the following table:
| Score | Academic Advising | Chromatic Dice | Cooperative Recon | Earth Observation | Manufacturer | Push Your Luck | Red‑finned Blue-eye | Wildlife Preserve | SUM |
|---|---|---|---|---|---|---|---|---|---|
| Baseline: Prost-2014 | 3.3 | 10.1 | 10.7 | 19.9 | 2.7 | 14.2 | 6.0 | 7.9 | 74.7 |
| Prost-DD-2 | 5.8 | 7.6 | 10.3 | 6.5 | 3.3 | 15.0 | 5.9 | 14.3 | 68.8 |
| Baseline: Prost-2011 | 3.2 | 12.8 | 9.0 | 18.7 | 7.1 | 6.3 | 6.9 | 3.9 | 67.9 |
| Prost-DD-1 | 6.6 | 7.5 | 12.0 | 5.3 | 2.8 | 12.7 | 5.4 | 14.3 | 66.5 |
| Random-Bandit | 0.7 | 17.1 | 1.5 | 12.8 | 4.1 | 13.1 | 5.6 | 10.8 | 65.6 |
| Conformant-SOGBOFA-B-IPC18 | 4.1 | 19.4 | 6.9 | 7.4 | 0.0 | 1.4 | 18.3 | 4.8 | 62.3 |
| Conformant-SOGBOFA-F-IPC18 | 4.9 | 18.9 | 6.4 | 7.1 | 0.0 | 1.3 | 18.7 | 4.8 | 62.1 |
| Imitation-Net | 0.0 | 3.8 | 0.0 | 0.6 | 0.3 | 8.8 | 5.0 | 10.1 | 28.6 |
| A2C-Plan | 1.4 | 0.6 | 4.8 | 1.6 | 2.7 | 6.9 | 4.8 | 3.8 | 26.6 |
Based on these results, we are proudly presenting the following awards for the discrete MDP probabilistic track of IPC 2018:
Winner
Prost-DDby Florian Geißer and David Speck
Runner-Ups
Random-Banditby Murugeswari Issakkimuthu, Alan Fern and Prasad Tadepalli
Conformant-SOGBOFA
by Hao Cui and Roni Khardon
Calls for Participation and Domains
Please forward the following calls to all interested parties.
Organizers
- Thomas Keller (University of Basel)
- Scott Sanner (University of Toronto)
- Buser Say (University of Toronto)